Metabolic networks as computation
2016-06-05
Tagged: software engineering, chemistry
Warning: half-baked ideas ahead.
Consider the metabolic network operating in your body. Your network has a lot of things going on. For example, it’s breaking down the molecules you eat, it’s synthesizing new molecules from the broken-down pieces, and it’s changing the concentrations of various signaling molecules, which in turn affect other parts of the network.
Your metabolic network has to adapt to outside factors: what you eat, what your body is doing, and so on. For example, a large intake of glucose raises insulin levels, which in turn causes glucose to be consumed by other parts of the metabolic network. Glucose levels then return to normal. In some sense, there’s computation going on: the network computes what actions are required to bring the system back to homeostasis.
This computation follows the laws of chemical kinetics. Differing concentrations of metabolites affect the rates of reactions that they’re involved in, and the sum of all of these reaction rates yields the net rate of change for that metabolite’s concentration.
To formalize this, I’ll describe a neural network that replicates the computation being done by a metabolic network.
In neural networks, each neuron typically takes in many inputs, combines them as a weighted average, and then applies an “activation function” to generate the final output.
Choices for activation functions vary widely. Here are some popular ones:
Rectified linear unit (zero when \(x < 0\))
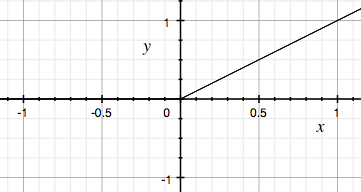
Hyperbolic tangent:
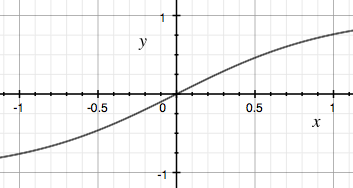
Here’s another activation function of my own invention: the Michaelis-Menten activation function.
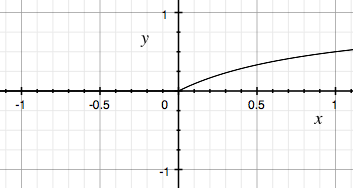
This one is somewhat like a cross between the ReLu and TanH functions. As its name suggests, it comes from the Michaelis-Menten equation for enzyme kinetics. You can think of the X axis as metabolite concentration and the Y axis as reaction rate.
Next, let’s define two types of neurons.
The first type of neuron is a concentration node. Its output describes the concentration of some metabolite. The second type is a reaction node. Its output describes a reaction rate.
Our neural network will have two layers of neurons (one concentration layer, one reaction layer), with each layer feeding into the other. The reaction nodes take the concentration nodes as input; after applying the MM activation function, the output is a set of reaction rates. Then, the concentration nodes take as input the reaction rates relevant to them, and in combination with their current value, they output a new concentration.
Voila! A neural network that models our metabolic network.
I’ve made a number of stretches, so the resulting neural network is not very similar to the neural networks everyone works with. One major caveat is that equations in chemical kinetics typically multiply their inputs, whereas traditional neural networks take linear combinations of their inputs. I suspect the differences will make it difficult to apply any lessons from neural networks to metabolism.
In any case, it’s a marvel that our body manages to cope with our diets at all!